这是一款考验你智商的三消,简单的消除技巧是不能达到每关制定任务的,这个游戏玩过的人都知道,让尽量多的同色连起来一起消,就能拿到很高的分数。但是实际执行起来,却有很大的难度。

为了方便我后面的讲解,我加入了坐标系,横排为a-j,竖排是0-9。

既然是数据流,当然要统计一下数字:
这一关里,从多到少分别是:黄色23个,蓝色21个,红色20个,绿色20个,紫色16个
一般人肯定会想,黄色数量最多,当然是想办法把黄色连起来才能获得分啦。
其实不一定,除了看数量多少之外,还要看他们的位置分布,能不能全部连起来……可能大家觉得很复杂,其实要说简单可以非常简单,关键在于:
【全连定理1】按列来数,数量少的优先看,位置靠下的优先看
按照这种想法,我们可以从下图看出一些端倪:
g列只有一个黄色,而且位置在h8这样一个靠下的位置,符合上面的定理,顺势再看看它能否与左右相连即可。详见下图:
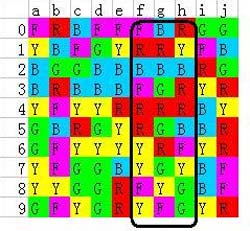
g8黄色靠左边,因为f8紫色的阻碍无法跟左边相连,而且不可能不消除黄色的前提下把f8紫色消掉,所以只能放弃
靠右边,h8-h9都是绿色,h7的黄色无论如何都无法跟h8的黄色相连,但是h1有一个黄色,理论上可以与g8的黄色相连。
这样一算下来,黄色23个不能全连起来,而且根据情况很有可能连第4名的20个都无法超过,所以我们退而求其次,看看第二名的蓝色能否胜任全连的任务。
照【全连定理1】所示,蓝色只有f列和j列是1块蓝色,而且都处于较高的位置!这无疑就是一个好消息。
撇除最右边的j列不看,f2蓝色的重要性明显更高。仔细看一下f2蓝色下方的其他星星,可以看出基本上都是2、2、2的组合,某种程度上并不适合微调;但是幸运的是e列的蓝色有3个,g列蓝色也有2个,所以从这里搭桥基本上没问题,预计搭桥后的效果如下图蓝色圈圈所示。
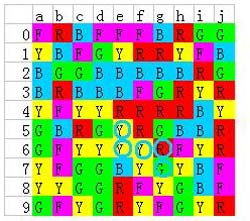
既然最容易断开的f列都已经解决了,那么剩下的其他列又有没有什么不可抗力导致无法全连呢?我们这就看看:
a b c d e f g h i j
2 2 2 2 3 1 2 2 4 1
a-d列都是只有2个,这就导致这几列的蓝色之间不能留下其他颜色的星星,所以重点就是看左上角的区域:

可以看到b列的绿、红、紫,c列的绿和紫都是关键的消除对象,所以优先考虑怎么把他们给消除了。
绿色最简单,b列和c列可以同时消去
b3的红色无法在不消除蓝色的前提下与b0的红色相连,所以只能找旁边——唯一一个红色就在c列,这很幸运,只要下降2格就能够到了。
c1的紫色,则需要下降3格才能与b4的紫色消除……这刚好是另一个关键消除对象。
根据以上信息,得出以下结论:
先点b2的绿色,然后分两条路:
1、b3红色下降两格,之后c列的紫色要下降3格;
2、c1紫色下降两格,之后b列的红色要下降4格,这时候问题就出来了:没办法让b列的红色单独下降4格而c列的红色不动,也就是这个方法没法消除红色!
于是,左上角的方案就出来了:
先消除b2的绿色:

再消除b6的紫色:

这样红色就连起来了~
然后立刻点掉红色?要知道点完红色,接下来要c列的紫色下降3格才能够到b列的紫色,而如果把红色先点了,c列的黄色就会堆到一起,这样你就无法让c列紫色下降3格了,所以在不影响红色的前提下,要先把c4的黄色点了:
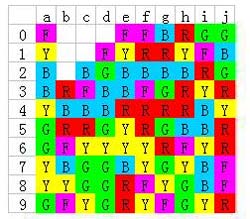
然后当然是把b列的红色给点掉:
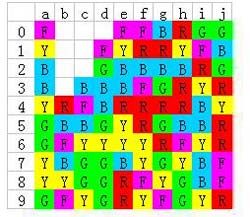
然后是c列下降2格,这很明显只有消除c7的绿色可以办得到
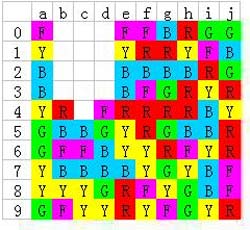
然后顺手把b6的紫色给点掉
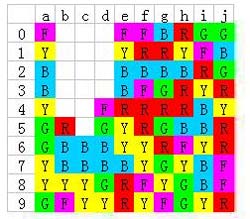
既然bcd列的蓝色都已经连起来了,然后当然就是想办法让a列的蓝色与bcd列的也连到一块,方法也简单,让a列相应降低3-5列都可以……
这么一来就有两种方法:
方法1:先消除a7的黄色,再消除a列绿色;
方法2:先消除a5的绿色,再消除a列黄色。
考虑到bc列已经没有绿色,万一在a列留下1个绿色会很麻烦;同样的,一旦消除a7的黄色块,bcd列都会没有黄色,对之后的全图消灭有很大的障碍。而方法1则是几乎没有后遗症,这实在不能不说是lucky。
所以,按照方法1先消除a7的黄色:
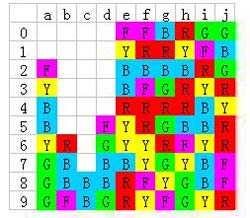
再消除a7的绿色:
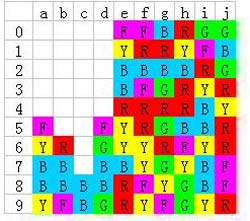
至此,左边的蓝色已经全部相连,接下来目标就是攻略右边的关键的“桥”了
在攻略桥之前,我们要顺便考虑一下左边已经完成的这一块,在消除蓝色之后如何完成全消。由于前面的大量分析,后期整理十分简单,如下图所示
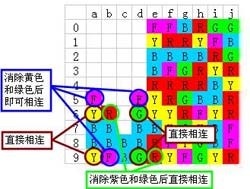
换句话说,e8-e9的两块红色,尽量不要消除,否则会影响到后面全消的难度
既然有这样一个目标,我们就开始第二部分的任务“搭桥”
首先,想办法让右边的桥都连起来。
e列有3个蓝色,
f列有1个蓝色
g列和h列都有2个蓝色
i列有4个蓝色
j列只有1个蓝色
因为gh列都只有2,且j列只有1,所以i列的4个依然只能直接相连才能达到全连的目的。
【全连定理】如果一列有3个以上的同颜色,那就代表隔壁一列未必要打竖相连
虽然有这么一个定理,但是g列和h列的蓝色之间相隔的都是可以直接消除的,所以就免了。在某些场合下,比如出现下图哪样的全连也是可以的:

回到我们这一题上,为了全连,我们先给右边作出规划:
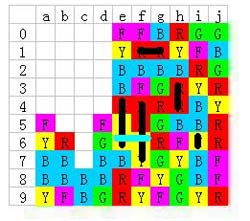
看图中黑色粗线,代表必须消除的星星。蓝色粗线则代表“桥”,因为f列的桥位置已经大致固定了,所以g列的2个蓝色,要有2-3个桥墩——也就是g3到g9之间这7个桥墩最起码要消除4-5个;
然后因为i列直接就有4个蓝色,所以h列的位置可以相对很宽松——只要跟g列相连就是了,也就是说h列有1-4个桥墩都没问题。
g1的红色可以直接消除;h3-h4的红色也可以直接消除;i8的黄色无法跟h7相连,不破坏蓝色的前提下,跟j4相连是最佳的选择。所以可以预订要么消除j5的红色,要么消除j7的紫色。
于是,我们下一步的行动有很多选择,只要选一个不要错得太厉害的就可以了:
消除e0紫色:
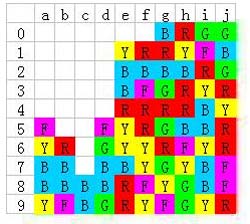
然后消除f1红色:
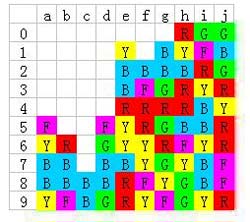
由于g列下面好几个都是无法直接消除的,尤其是g6的红色,所以这一步建议把h8的绿色给消除掉,这样g6红色就有救了:

然后,按照之前所说的,让j4的黄色下降2格:
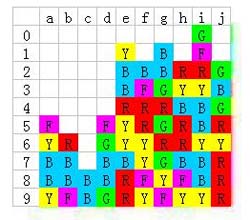
然后顺手把i6的黄色消掉:
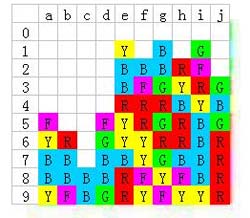
右边的桥墩也准备完成了,开始向中间搭桥,把g6红色消除:
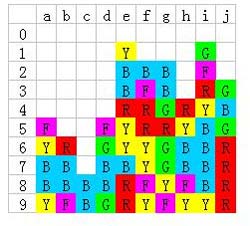
然后是e4红色:
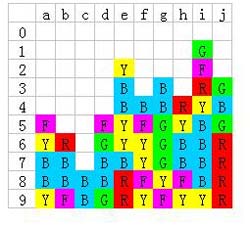
接下来是e5的黄色和g5的绿色
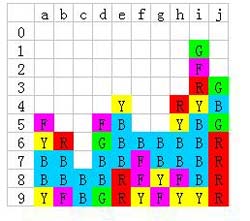
当然少不了的是把最右边的蓝色也拉到一块,这么一来,蓝色就完成了全连!
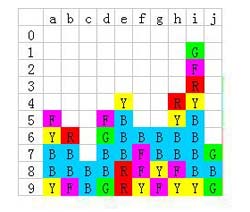
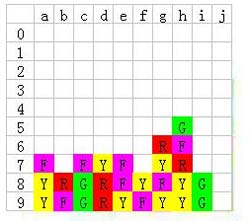
全部蓝色消除之后,剩下的就好办了:左边按照之前的方案,可以顺利地完成到下图所示:
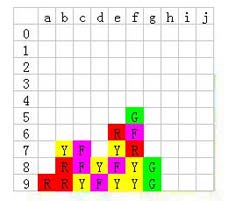
右边的绿色明显要等连起来再一锅端的,所以先消除e9的黄色,让d9的紫色连起来:
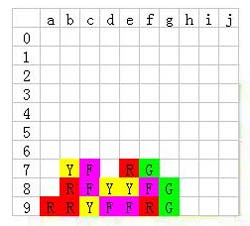
f8的紫色位置很尴尬,只能跟c7c8的紫色一起消;所以现在先把a9的红色和d9的紫色消除
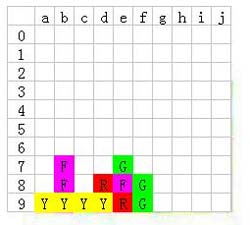
剩下的,相信玩过的人都懂的。
先消除黄色,然后是红色和绿色,最后紫色~
21个全连+全图消除,这样一关少说也有6000分以上
当然,有些关卡的星星位置实在太差,导致无法全连和全图消除也是有可能的,但是以上面的方法加上足够多的时间分析,制造尽量多全连和尽量全消,将分数保持在3000分以上还是有可能的。






 关注游戏狗订阅号
关注游戏狗订阅号