梦幻西游手游封印命中概率实战测试说明

梦幻西游手游封印命中概率实战测试说明，对于一个分布确定随机变量X，我们要去测试他的概率分布，就要通过不断的试验来估计他的分布，这就好比有个黑盒子，里面有一些红球和一些白球，那到底红球白球的比例是多少呢?我们通过不断的摸球就能大概知道里面的情况了。当然，我们摸得越多就相对越了解盒子里的情况。这也好比我们在一个行业摸爬滚打，一开始我们对这个行业的情况一无所知，随着我们不断的积累经验，我们对这个行业的认知会越来越准确一样，当然我们的认知很有可能有偏差，但这个偏差总是随着时间的增加越来越小的。

在数学上有个定理叫做大数定理。讲的是，当试验次数增大的时候，试验测得的频率会逐渐逼近被试验对应随机变量的真实概率，这个逼近真实概率的速度是正比于1/根号N的，其中N是试验的次数。比如我测100次得到的结果可能和真实概率的误差是10%，那么我测10000次得到的结果和真实结果的误差就会降低到10%/10=1%。

还有另一个定理叫做中心极限定理，讲的是，对任意一种概率分布，对他不断试验，抽样结果的平均值的分布，随着试验次数的增加会逼近为一个正态分布。

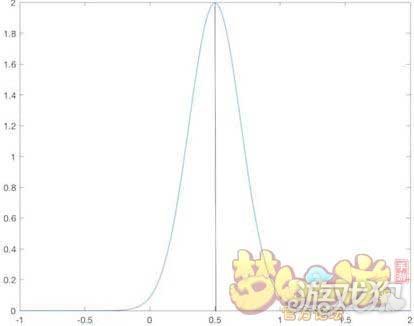
打个比方，大家来看上面这两个图，那个竖线是真实的概率，而曲线上的点对应的横坐标就是我们可能测到的概率(n个数据的平均值)，随着测量次数的增加，这个曲线会越来越窄，最后我们测得的概率就会越来越接近那个竖线

我们把这两个定理结合到一块就是，我们可以通过不断试验来估算封印命中的真实概率，估算方法是封印命中记1，封印失败记0，然后求这些0和1的平均值。这个平均值会在真实的封印概率附近分布，分布的情况由中心极限定理可以知道，是一个接近正态分布的分布，而这个正态分布的标准差-由大数定理可以到 随着1/根号N衰减。

特别的，对于一组测得的N个数据{X_n},平均值是u,标准差是sigma,那么这组数据的测量偏差是sigma/根号N，由于只有在N非常非常大的时候这个测量平均值u才满足正态分布，所以对于次数比较小的时候，这个测量平均值满足的是自由度N-1的t-分布，所以这个测量偏差需要再乘上一个修正系数K。所以最后我们通过测量平均值去估计真实概率会有 k*sigma/根号N的误差。

这个k和次数N和我们选择的置信概率有关。例如，对于95%置信概率，N=400的t-分布，k=1.97。意思就是真实的封印概率有95%的概率落在我们测的

[u-1.97*sigma/根号(400),u+1.97*sigma/根号(400)]这个区间里。